The minimum number of domain controllers in a domain is ______

Which of the following is the fastest way to create a report?

a. Report tool b. Report Wizard c. Report Design d. Blank Report

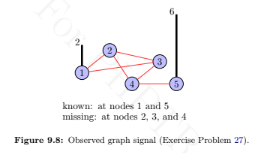
This problem demonstrates the use of Laplacian quadratic form for interpolation on graphs. Consider an observed graph signal, shown in Figure 9.8, where signal values at nodes 2, 3, and 4 are missing. The aim of interpolation is to fill in the missing values. One criteria for estimating the missing values is to minimize the squared sum of the differences in signal values between the neighboring vertices, which is nothing but the quadratic form of the graph Laplacian. Therefore, the interpolation problem can be written as

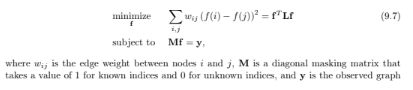
signal with zeros at missing indices. For example, if the values at nodes 2, 3, and 4 are

missing, the masking matrix is

M = diag {1,0,0,0,1} and the observed graph signal can be

written as y = [2, 0, 0, 0, 6] T. Find the missing values in the observed graph signal by solving

the above optimization problem. Hint: Use the method of Lagrange multipliers.