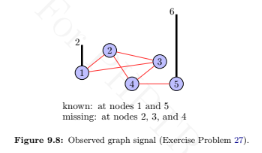
This problem demonstrates the use of Laplacian quadratic form for interpolation on graphs. Consider an observed graph signal, shown in Figure 9.8, where signal values at nodes 2, 3, and 4 are missing. The aim of interpolation is to fill in the missing values. One criteria for estimating the missing values is to minimize the squared sum of the differences in signal values between the neighboring vertices, which is nothing but the quadratic form of the graph Laplacian. Therefore, the interpolation problem can be written as
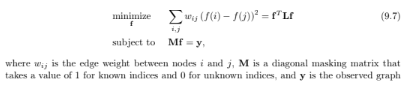
signal with zeros at missing indices. For example, if the values at nodes 2, 3, and 4 are
missing, the masking matrix is
M = diag {1,0,0,0,1} and the observed graph signal can be
written as y = [2, 0, 0, 0, 6] T. Find the missing values in the observed graph signal by solving
the above optimization problem. Hint: Use the method of Lagrange multipliers.

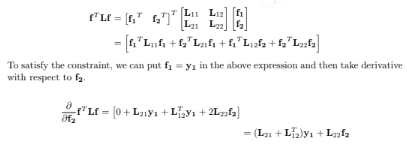

You might also like to view...
________ is a formula that multiplies the contents of cell D5 by the contents of cell E7
A) &D5*E7 B) =D5*E7 C) #D5*E7 D) D5*E7
Case-Based Critical Thinking QuestionsCase 2-2You are writing a brief manual on Web page design and you are reviewing the guidelines section you've written. What do you tell readers is the range for relative font sizes?
A. small to large B. xx-small to xx-large C. 1 to 7 D. 1 to 8