You have $64 to spend on fish (F) and chips (C). Suppose the price per unit of fish (Pf) is $8 and the price of chips (Pc) is $2. Your utility function for fish and chips is given as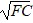 
such that MUc. = andMUF = 
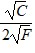are the marginal utilities of F and C. How many units of C and F should you buy to exhaust all income and to maximize utility?
What will be an ideal response?
First, in order to maximize utility, you have to be at equilibrium. This means that the following condition has to be satisfied: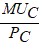
= 
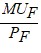
It is better to write this as:
MUC.PF = MUF.PC
Now substitute the corresponding values in the above expression: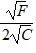
. $8 - 
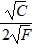$2
Canceling the 2s in the denominator and cross-multiplying, we get
C = 4 F.
Now, the second aspect of this is your income of $64 that has to be spent on F and C. Therefore, the budget constraint should satisfy this condition:
64 = C Pc + F Pf or
64 = 2C + 8F, and now from the previous condition, we have
64 = (4F) 2 + 8F or
F = 4 units.
C = 16 units and total utility is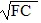
= 
= 
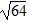= 8 utils.
You might also like to view...
Who does the government borrow from?
What will be an ideal response?
If you are willing to pay no more than $4 for a slice of pizza and the price of a slice of pizza is $4, then
A) if you buy it, you would be cheated because you would realize no total benefit from the purchase. B) you buy it but you get no marginal benefit from the purchase. C) you will not buy it. D) you buy it but you get no consumer surplus from the purchase. E) you might buy it depending on how the slice's marginal benefit compares to its price.