The Grubbs’ test, which is described by Algorithm 10.1, is a more statistically sophisticated procedure for detecting outliers than that of Definition 10.3. It is iterative and also takes into account the fact that the z-score does not have a normal distribution. This algorithm computes the z-score of each value based on the sample mean and standard deviation of the current set of values. The value with the largest magnitude z-score is discarded if its z-score is larger than gc, the critical value of the test for an outlier at significance level ?. This process is repeated until no objects are eliminated. Note that the sample mean, standard deviation, and gc are updated at each iteration.

(a) What is the limit of the value m??1
m
t2
c
m?2+t2
c
used for Grubbs’ test as
m approaches infinity? Use a significance level of 0.05.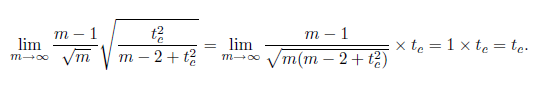

(b) Describe, in words, the meaning of the previous result.

(a) Note that this could have been phrased better. The value of this ex-

pression approaches tc, but strictly speaking this is not a limit as tc

depends on m.



Also, the value of tc will continue to increase with m, although slowly.

For m = 1020, tc = 93 for a significance value of 0.05.

(b) The distribution of g is becomes a t distribution as m increases.