Consider player n in a sequential game.
a. If the player can play 2 actions from a single node, how many pure strategies does he have?
b. Suppose he can play 2 actions at each of two different nodes. How many pure strategies does he have now?
c. Suppose he can play 2 actions at each of three different nodes. How many pure strategies does he have now?
d. Suppose he can play 2 actions at each of four different nodes. How many pure strategies does he have now?
e. Suppose he can play 2 actions at each of k different nodes. How many pure strategies does he have now?
What will be an ideal response?
a. He simply chooses one of his two actions -- and thus has 2 possible strategies.
b. Suppose the actions at each node are L and R. Then his strategies are (L,L), (L,R), (R,L), (R,R) -- so he has 4 possible strategies.
c. We now have to specify an action for each of 3 nodes. The portions of the strategies for the last two nodes are the same as the strategies in (b) -- but now he combines those with either playing L or R in the first stage. Thus, we now have 8 possible strategies.
d. The portions of the strategies for the last 3 nodes are now the same as the strategies if there were only 3 nodes -- i.e. there are 8 of those (as determined in (c)). But now the player has to combine these with either L or R in the first stage -- giving us 16 possible strategies.
e. Following the pattern developed in (a) through (d), the number of strategies is now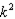 .
.
b. Suppose the actions at each node are L and R. Then his strategies are (L,L), (L,R), (R,L), (R,R) -- so he has 4 possible strategies.
c. We now have to specify an action for each of 3 nodes. The portions of the strategies for the last two nodes are the same as the strategies in (b) -- but now he combines those with either playing L or R in the first stage. Thus, we now have 8 possible strategies.
d. The portions of the strategies for the last 3 nodes are now the same as the strategies if there were only 3 nodes -- i.e. there are 8 of those (as determined in (c)). But now the player has to combine these with either L or R in the first stage -- giving us 16 possible strategies.
e. Following the pattern developed in (a) through (d), the number of strategies is now
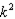 .
.
Economics
You might also like to view...
What is the conclusion that behavioral economists have made about the amount of product variety in the market place?
What will be an ideal response?
Economics
Refer to Figure 12-4. If the market price is $30, should the firm represented in the diagram continue to stay in business?
A) No, it should shut down because it cannot cover its variable cost. B) Yes, because it is making a profit. C) No, it should shut down because it is making a loss. D) Yes, because it is covering part of its fixed cost.
Economics