Suppose the market demand curve is as depicted in the graph, and all firms have constant
1
1
24
////AA==
marginal costs of 20. Assume that consumer tastes in x are quasilinear.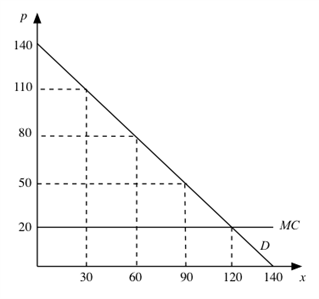                                
a. If a single monopolist who does not price discriminate serves this market, what is the value of consumer surplus and monopoly profit?

b. Suppose the government imposes a price ceiling of 40 on the monopolist from part (a). How does this change the value of consumer surplus and monopoly profit?
c. Suppose instead that this market has two Cournot competitors. Illustrate their best-response functions (labeling intercepts and slopes) as well as the Nash equilibrium. What is the value of consumer surplus and profit in the market now?
d. If the same price ceiling of 40 is imposed on the Cournot oligopoly, how will the best response functions change? (Assume that, if there is a good that is produced but does not get bought, it is equally likely that firm 1 gets stuck with the good as it is that firm 2 gets stuck with it, and it costs at least a penny to dispose of a good you are stuck with.) Is there more than one possible Nash equilibrium?
e. Will overall surplus increase?
f. Does your answer to (e) change if the price ceiling is imposed on Bertrand price competitors?g.  True or False: Whenever price ceilings impact the price at which goods are traded, they disturb the price signal and therefore result in deadweight losses.

What will be an ideal response?

   CS = 60(60)/2 = 1,800
   Profit = 60(60) = 3,600

  

b. The monopolist now produces 100 at the price 40. This implies

   CS = 100(100)/2 = 5,000
   Profit = 20(100) = 2,000

c. Each firm now produces 40 - for a total output of 80 in the market. At output of 80, the price is then 60 (as read off the demand curve). Thus,

   CS = 80(80)/2 = 3,200
   Profit = 30(90) = 3,200

d. Firm 1's best response to firm 2 not producing at all is to produce 100 when the price ceiling is set to 40. If firm 2 produces 1 unit, then firm 1's best response is to reduce its output to 99. (If it produced 100 in response, there would be a 50% chance of being stuck with the good and incurring a cost of at least 20.01 and a 50% chance of selling the good at a profit of 20. In expectation, it is therefore not a best response to continue to produce 100.) The same reasoning continues to hold - implying a best response function with intercepts of 100 on both axes. The same is true for firm 2. Thus, the best response functions overlap, with the two firms dividing output of 100 in any way being a Nash equilibrium.



e.        CS = 100(100)/2 = 5,000

   Profit = 20(100) = 2,000



Yes, overall surplus increases from 6,400 to 7,000.

f.  Under Bertrand competition without a price ceiling, 120 units of output would be produced at a price of 20. This would imply CS of 120(120)/2 = 7,200 and zero profit for the firms. Under the price ceiling, the Bertrand price equilibrium is for both firms to charge 40 - implying CS = 100(100)/2 = 5,000 and Profit = 20(100) = 2,000 just as in the Cournot case. But now surplus decreases (from 7,200 to 7,000) when the price ceiling is imposed.



g.  The statement is true only perfectly competitive markets. When prices are already distorted (through, for instance, market power - as in this example) a price ceiling can, if properly placed, reduce or eliminate deadweight loss from the existing distortions.