The n?bit two’s complement integer N is written an?1, an?2, . . . a1, a0. Prove that (in two's complement notation) the representation of a signed binary number in n + 1 bits may be derived from its representation in n bits by repeating the leftmost bit. For example, if n = ?12 = 10100 in five bits, n = ?12 = 110100 in six bits.
What will be an ideal response?
In n bits the positive number N is represented by an?1, an?2, . . . a 1, a0. We can extend this to n+1 bits by appending a 0 to the left without changing its value; that is 0, an?1, an?2, . . . a 1, a0.
Now consider the value ?N in n bits. This is represented as 2n ? N. If we extend this to n + 1 bits, it becomes 2n+1 ? N or 2n + 2n ? N. This is, of course, the original negative representation with a leading 1 to the left. Consequently, a positive number is extended by appending a 0, and a negative number by adding a 1; that is, by extending the sign bit.
You might also like to view...
What decisions were made? Why? What are the advantages and disadvantages of this particular test plan?
Given the following subsystem decomposition:
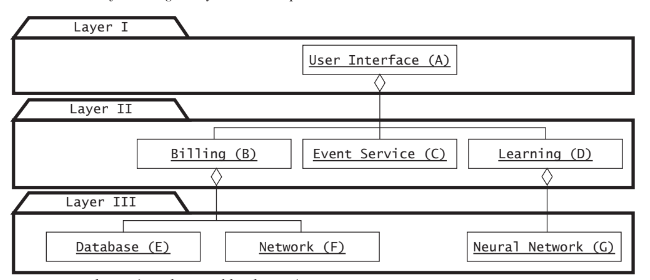
comment on the testing plan used by the project manager: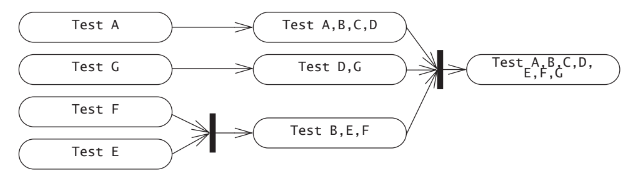
The ____________________ is an international community of over 400 organizations dedicated to developing new protocols and specifications to be used with the Web and to ensure its interoperability.
Fill in the blank(s) with the appropriate word(s).