Given the set of cluster labels and similarity matrix shown in Tables 8.4 and 8.5, respectively, compute the correlation between the similarity matrix and the ideal similarity matrix, i.e., the matrix whose ijth entry is 1 if two objects belong to the same cluster, and 0 otherwise.

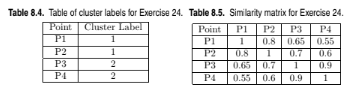
We need to compute the correlation between the vector x =< 1, 0, 0, 0, 0, 1 >
and the vector y =< 0.8, 0.65, 0.55, 0.7, 0.6, 0.3 >, which is the correlation

between the off-diagonal elements of the distance matrix and the ideal simi-
larity matrix.
We get:
Standard deviation of the vector x : ?x = 0.5164
Standard deviation of the vector y : ?y = 0.1703
Covariance of x and y: cov(x, y) = ?0.200
Therefore, corr(x, y) = cov(x, y)/?x?y = ?0.227