If country A had four times the initial level of real GDP per capita of Country B and it was growing at 1.4 percent a year, while real GDP was growing at 2.3 percent in country B, how long would it take before the two countries had the same level of real GDP per capita?
Ans: Let country B's initial GDP be x. Then country A's initial GDP will be 4x
Let time taken when they have same gdp be t
thus, x*(1.023)^t = 4x*(1.014)^t
(1.023)^t = 4*(1.014)^t
taking log on both sides
t log 1.023 = log 4 + t log 1.014
0.00987 t = 0.60206 + 0.00604t
1.
0.00987t - 0.00604t = 0.60206
0.00383t = 0.60206
t = 0.60206/0.00383 = 156.88 years
Thus, it will take 156.88 or aproximately 157 years for the GDP to be same
You might also like to view...
Caroline has saved $100,000 for her retirement. She earned 4 percent interest on that money during the year 2013. If the inflation rate was 1 percent in 2013, what was Caroline's real interest rate?
A) $4,000 B) 5 percent C) 1 percent D) 4 percent E) 3 percent
Refer to the information provided in Table 33.3 below to answer the question(s) that follow. Table 33.3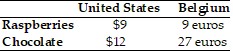
Refer to Table 33.3. If the exchange rate is $1 = 3 euros, then
A. the United States will import both raspberries and chocolate. B. the United States will import chocolate and Belgium will import raspberries. C. the United States will import raspberries and Belgium will import chocolate. D. Belgium will import both raspberries and chocolate.