Suppose the economy's production function is Y = A(300N - N2). The marginal product of labor is MPN = A(300 - 2N). Suppose that A = 10. The supply of labor is NS = 0.05w + 0.005G.(a)If G is 26,000, what are the real wage, employment, and output?(b)If G rises to 26,400, what are the real wage, employment, and output?(c)If G falls to 25,600, what are the real wage, employment, and output?(d)In cases (b) and (c), what is the government purchases multiplier; that is, what is the change in output divided by the change in government purchases?
What will be an ideal response?
| (a) | Setting labor supply equal to labor demand gives N = 0.05 × 10 × (300 - 2N) + 0.005G, which |
Then w = 10 × [300 - (2 × 140)] = 200 and Y = 10 × [(300 × 140) - 1402] = 224,000.
| (b) | Following the same procedure gives N = 141, w = 180, and Y = 224,190. |
| (c) | N = 139, w = 220, and Y = 223,790. |
| (d) | In part (b), the multiplier is 190/400 = 0.475. In part (c), the multiplier is 210/400 = 0.525. |
You might also like to view...
Refer to Table 16.1. Which of the following statements is correct?
A) There are potential gains from trade if: (1 ) Mexico specializes in the production of tomatoes, (2 ) Guatemala specializes in the production of beer, and (3 ) Mexico trades tomatoes to Guatemala for beer. B) There are potential gains from trade if: (1 ) Mexico specializes in the production of beer, (2 ) Guatemala specializes in the production of tomatoes, and (3 ) Mexico trades beer to Guatemala for tomatoes. C) There are no potential gains from trade because Mexico has an absolute advantage in the production of beer and tomatoes. D) There are no potential gains from trade because Guatemala has an absolute advantage in the production of beer and tomatoes.
Refer to the given data. We can conclude from the information given that this firm is a:
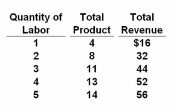
A. pure monopolist.
B. discriminating monopolist.
C. monopolistic competitor.
D. pure competitor.