The ‘Transfer’ transactions T and U are defined as:

T: a.withdraw(4); b.deposit(4);



U: c.withdraw(3); b.deposit(3);



Suppose that they are structured as pairs of nested transactions:





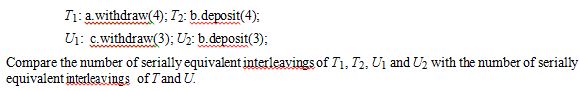
Explain why the use of these nested transactions generally permits a larger number of serially equivalent interleavings than non-nested ones.

Considering the non-nested case, a serial execution with T before U is:
![13465|551x142](upload://wukCemgBKCpOGU52WpQmpxDtdy1.jpg
We can derive some serially equivalent interleavings of the operations, in which T’s write on B must be before
U’s read. Let us consider all the ways that we can place the operations of U between those of T.

All the interleavings must contain T2; U2. We consider the number of permutations of U1 with the operations
T1-T2 that preserve the order of T and U. This gives us (3!)/(2!*1!) = 3 serially equivalent interleavings.
We can get another 3 interleavings that are serially equivalent to an execution of U before T. They are different because they all contain U2; T2. The total is 6.
Now consider the nested transactions. The 4 transactions may be executed in any (serial) order, giving us 4! =
24 orders of execution.

Nested transactions allow more serially equivalent interleavings because: i) there is a larger number of serial executions, ii) there is more potential for overlap between transactions (iii) the scope of the effect of conflicting operations can be narrowed.