Consider a market with inverse demand p = 100 – 2Q. Firms have no fixed cost and constant marginal cost c
a. Derive the firms' outputs and profits when this market is served by Cournot duopolists.
b. How do outputs and profits vary with c? Specifically, use calculus to find the derivative of the output of each firm and profit of each firm with respect to c.
c. Suppose the firm's also have a fixed cost of F in addition to the marginal cost c. How does F alter the best response functions and NE? Explain in words. (For technical reasons, assume that both firms still produce a positive level of output in equilibrium)
a. First, the profit for firm 1 is:
π1 = (100 – 2q1 – 2q2 )q1 – cq1
To find the best response, take derivatives and set equal to zero:
100 – 4q1 – 2q2 – c = 0
Rearranging to get:
q1 = (100 – c – 2q2 )/4
The objective function for each firm is identical, implying that in equilibrium q1=q2. Use this to solve
q1 = q2 = (100 – c)/6
b. dq/dc = -1/6 → output per firm decreases as c increases.
Profit is:
2(100-c)2/36
The derivative is -4(100 - c)/6 < 0. Thus, profit decreases as c increases.
c. The fixed cost will not alter the best response functions if small. This is because it does not remain in the derivative of the profit function.
You might also like to view...
A worker's contribution to the firm's revenue is measured directly by the worker's: a. value of marginal product
b. marginal product multiplied by his/her wage. c. marginal product minus his/her wage. d. contribution to total output.
Refer to the graph shown. If the price were at the market equilibrium price, the total surplus would be equal to: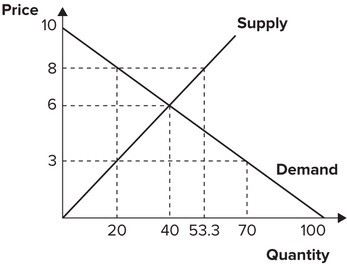
A. 400. B. 120. C. 80. D. 200.