At least how many keys must be inserted so that the left node in the middle level would split?

Consider the following B+ tree:

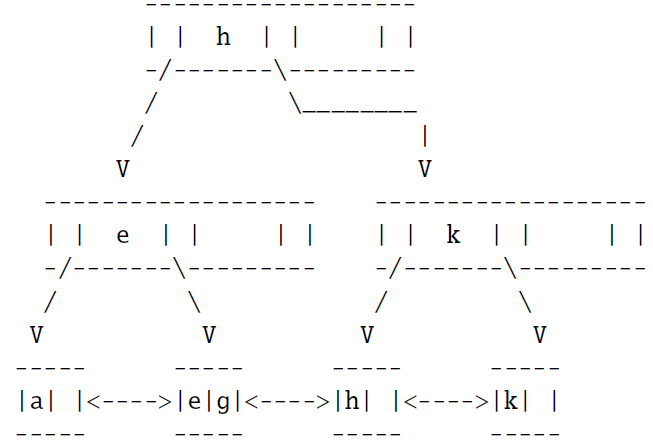
Here we are interested in the least number of keys that are required to affect a split in m1. Therefore we should try to add keys in a manner that will cause node splits as quickly as possible.

Adding a key to n2 will cause a split into n21 and n22 with n22 having one free spot and n21 being full. A separator key will be pushed up to m1 filling up the remaining free slot there. Adding a key to n21 will cause a split in that node and will necessitate a push-up of a separator key to m1. This will overflow m1 and cause a split.