Suppose that you are given a cost function c(w,r,x)=2w1/2r1/2x3/2 where w is the wage rate for labor, r is the rental rate of capital and x is the output level.
a. Does the production process that gives rise to this cost function have increasing, decreasing or constant returns to scale?
b. Derive the marginal cost function.
c. Calculate the supply function for the firm - i.e. the function that tells us for every combination of input and output prices, how much the firm will optimally produce. How does output by the firm change as input and output prices change?
d. If the cost function had been c(w,r,x)=2w1/2r1/2x1/2 instead, how would your answer to (c) change? How can that make any sense?
What will be an ideal response?
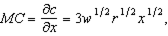and the derivative of this with respect to output is positive -- i.e. the MC curve is upward sloping. This implies decreasing returns to scale.b. We derived it above as
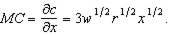(Part (a) could be answered without making explicit reference to the MC function.)c. The supply function can be derived by setting MC equal to price and solving for output. (Recall the supply curve is the part of the MC curve that lies above AC -- and since we know this production process to have decreasing returns to scale throughout, the MC lies above AC everywhere.) Solving
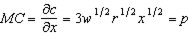
gives the supply function
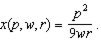
d. In that case, the production process has increasing returns to scale (with downward-sloping MC). As a result, the firm's profit maximization problem does not have an interior solution -- the firm would produce an infinite amount. Of course this does not make sense -- because it does not make sense to assume price-taking firms can have production technologies that have increasing returns to scale throughout.
You might also like to view...
Suppose the government of a town of 2,000 people implements a tax on each of its 2,000 citizens to raise $1,000 for a sculpture that will be placed in the common area of a 5-person neighborhood
Each of the 5 people in the small neighborhood will receive $120 in benefits from the sculpture. This tax is likely to A) generate a great deal of opposition from taxpayers. B) generate a great deal of opposition from the 5 people in the affected neighborhood. C) generate little opposition from a majority of its taxpayers. D) generate the desirable social outcome.
According to classical theory, a shift in aggregate demand will affect
A) the price level only. B) real Gross Domestic Product (GDP) only. C) the level of employment only. D) both real Gross Domestic Product (GDP) and the level of employment.