A beekeeper society is interested in the production of honey in a region, and have theorized that honey production is a function of the number of bees in a hive, whether the farms near the hive use pesticides, and the local temperature. Perform an ordinary least squares regression on the following data, with honey production being the dependent variable, and plot the residuals in space. Do they show signs of autocorrelation? Use an added variable plot to determine whether they should also include the distance between the hives and a local orchard located at (8,10) in their regression. Run the regression again with the new variable and compare the r2 values and standard errors.

What will be an ideal response?

The regression equation associated with the data is given by

Honey = 142.3 Xtemp -430.6 Xpesticide + 7.1 Xbees + 95.201

Of these, only the number of bees appears to be significant to the equation, which has a relatively

low r2

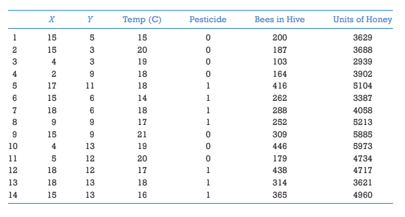
value of .629 with a standard error of 656.1. The pattern of the residuals does suggest

autocorrelation:



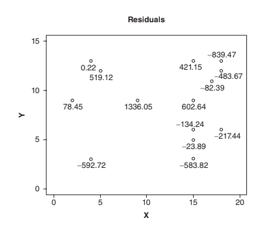
Thus we calculate the distance between each of the locations and the orchard and regress this

variable on the x values. We compare the two sets of residuals and produce the following added

variable plot:



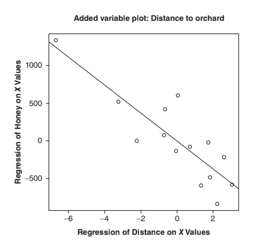
There is a distinct linear trend, which leads us to suspect that we should include the variable in our

regression. Doing so, we find the next regression equation:

Honey = 142.8 Xtemperature - 212.4 Xpesticide + 7.4 Xbees + 1309.3

The r2

value is much higher at .9, and the standard error is 358.3, which is much lower.