Consider the simultaneous choice game represented by the matrix below where Player A chooses either Up or Down and Player B chooses either Left or Right.

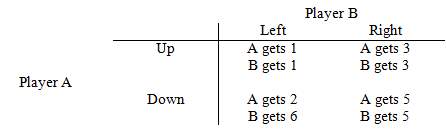
i. Discuss whether or not either player has a dominant strategy.

ii. Identify the Nash equilibrium in the game and explain why you have concluded that it is a Nash Equilibria.

iii. Now imagine that the game could be played sequentially. If Player A gets to choose their strategy first, can they do better than in the sequential game than in the equilibrium from the simultaneous game? Explain.

i. Player A has a dominant strategy of choosing Down. Player B does not have a dominant strategy.
ii. The Nash Equilibrium is for Player A to choose Down and Player B to choose Left. This is because from A’s perspective, 2 > 1 and from B’s perspective 6 > 5.
iii. If Player A chooses Up, then Player B will select Right since 3 > 1. If Player A chooses Down, then Player B will choose Left since 6 > 5. So, if Player A chooses Up, they will ultimately get a payoff of 2 whereas by choosing Up, they will get a payoff of 3. Therefore, Player A can be better off in the sequential game because it gives them the ability to credibly commit to playing Up, the result of which is a payoff of 3 rather than the payoff of 2 that they earn in the Nash equilibrium of the simultaneous game.