Consider the following two investments. One is a risk-free investment with a $100 return. The other investment pays $2,000 20% of the time and a $375 loss the rest of the time. Based on this information, answer the following: (i) Compute the expected returns and standard deviations on these two investments individually. (ii) Compute the value at risk for each investment. (iii) Which investment will risk-averse investors prefer, if either? Which investment will risk- neutral investors prefer, if either?
What will be an ideal response?
(i) The expected rate of return is $100 for the risk-free investment. The risk-free investment has a standard deviation of zero because the return is certain. For the risky investment:
Expected return = 0.2($2,000) + 0.8(-$375) = $100
Standard Deviation = 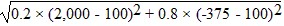 2 =
2 = 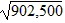 = 950
= 950
(ii) The value at risk for the risk-free investment is $100 because it pays a certain return. The value of risk for the risky investment is -$375, this is the maximum amount the investor can lose.
(iii) The risk-averse investor will prefer the risk-free investment. The risk-neutral investor will not have a preference between the two investments because they pay the same expected return.
You might also like to view...
When taxes paid by a check are deposited in tax and loan accounts,
A) bank reserves and the money supply are unaffected. B) bank reserves fall but the money supply is unaffected. C) bank reserves are unaffected but the money supply falls. D) bank reserves and the money supply fall.
Tina's marginal utility of her first piece of cake is 15, while Jerry's marginal utility of his first piece of cake is 24 . An economist would conclude that:
a. Tina likes cake more than Jerry likes cake. b. Jerry likes cake more than Tina likes cake. c. Tina likes cake less than Jerry likes cake. d. Jerry likes cake less than Tina likes cake. e. we can't make a comparison to see who values cake more.