Suppose we live in an exchange economy with two goods. I own 50 of both goods, and you own 250 of both goods. My tastes are captured by the utility function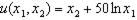 
and yours are captured by the utility function 
.
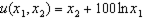a. Calculate the competitive equilibrium price.
b. How much do each of us consume of good 1 in equilibrium?
c. Suppose the government transfers 100 units of your good 1 endowment to me. How is your answer to (a) and (b) affected?
d. Suppose the government instead transfers 100 units of good 2 from you to me. How is your answer to (a) and (b) affected?
e. Do you think your answers to (c) and (d) generally hold for most types of tastes -- or do you think they arise because of some specific feature of these tastes?
What will be an ideal response?
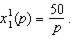Doing the same for you gives us your demand as 
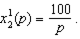Adding them and setting them equal to the economy's endowment of good 1 (which is 300), we get the equilibrium price p*=0.5.b. Plugging this price back into the demand functions from part (a), we get my consumption as 100 and yours as 200.
c. The demand functions for good 1 are independent of the endowments -- thus nothing would be different in terms of good 1 consumption.
d. The same answer as (c).
e. The result is due to the quasilinearity of good 1 -- which makes demands for good 1 independent of endowments. As a result, there is no wealth effect relative to good 1 -- and redistributions of endowments do not change the equilibrium prices or quantities.
You might also like to view...
Strategic dependence is found in
A) monopoly markets. B) oligopolistic markets. C) monopolistic competitive markets. D) perfect competitive markets.
Pa and Pb represent the prices that citizens (a) and (b), the only two people in this nation, are willing to pay for additional units of a quantity (Qc) of the public good. Qs represents the quantity of the public good supplied by government at each of the collective prices.QcPaPbQs1$4$552344324342325121Refer to the above information. If only 1 unit of this public good is produced, then the marginal benefit is:
A. $4 and the marginal cost is $7. B. $3 and the marginal cost is $9. C. $9 and the marginal cost is $3. D. $6 and the marginal cost is $3.